DOVI-LOG | 그래프 탐색 알고리즘

개요

개발하거나 애니만 보는 요즘, 두뇌회전이 활발하지 않다는 것을 느꼈습니다. 알고리즘이나 풀어볼까? 하는 생각에 문득 dfs에 대해 공부하고 싶어졌고 이를 바탕으로 알고리즘 문제도 풀어보았습니다. 그럼 출발할게요!

그래프 탐색이란?

dfs에 대해 알기 전, 그의 기본개념인 그래프 탐색에 대해 알 필요가 있습니다. 그래프 탐색이란 트리 그래프 구조에서 노드와 간선을 탐색하는 알고리즘입니다. 특정 순서를 두고 어떤방식으로 탐색할 것인지에 대해 해결할 때 사용합니다. 종류로는 오늘 설명할 dfs와 추후 다른 글로 설명할 bfs가 있습니다. 그럼 dfs에 대해 정리해봅시다.

dfs란?

dfs는 경로기반의 문제를 해결할 때 사용하는 그래프 탐색 알고리즘이며, 자식 노드를 우선 방문하여 더 이상 노드가 없을 때 까지 탐색합니다. 그러면 back tracking(역추적)을 통해 다시 상위 노드로 돌아간 후, 방문하지 않는 노드를 탐색합니다.

구현 방식으로는 대표적으로 스택과 재귀함수로 구현할 수 있습니다. 특징으로는 앞서 말씀드렸듯 노드를 깊이 탐색하기에 경로 기반 문제에 유리하며, 방문한 노드를 기록하고 있어서 무한루프를 방지할 수 있습니다.

그럼 사진을 갖고와 보도록 하겠습니다. 예제로 동작과정을 이해해봅시다.

동작과정

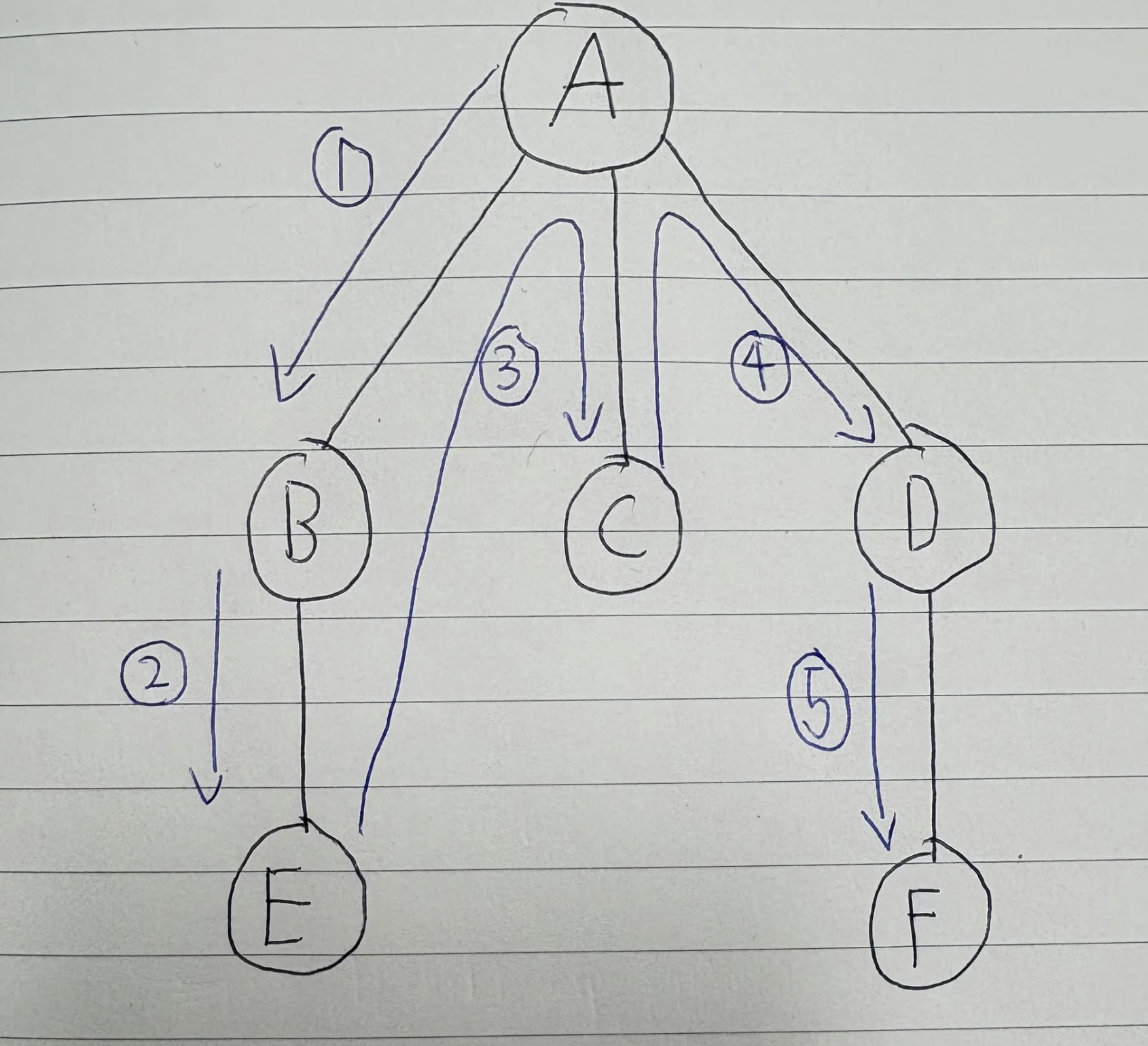
dfs 사진 제가 그린 트리입니다 ㅎㅎ, 암튼 저는 재귀함수로 동작과정을 설명하겠습니다. 왜냐하면 back tracking에 대해 따로 구현할 필요가 없기도 하고 재귀를 통해 머리를 좀 굴러볼 겸해서…

1. 탐색을 시작할 초기 노드 설정

해당 노드부터 탐색을 시작하게 됨

2. 노드 방문

방문한 노드에 대해 방문기록을 남김
이때 visited 객체나 배열을 만들어서 사용해야함 ex) { A: false, B: false, C: false ….}

3. 연결 노드 방문

현재 노드의 연결된 노드들을 순회함
순회할 때는 방문한 적이 없는 연결노드들만 탐색 (visited 객체나 배열을 참조하여 탐색하는 조건문 추가)

4. dfs 재귀 호출

방문하지 않는 연결노드에 대해 dfs를 재귀함수로 구현해 해당 연결노드와 또 연결된 노드들이 있는지 탐색을 이어감

5. Back Tracking(역추적)

연결노드가 없으면 다시 상위 노드로 올라가고 다음 노드를 탐색함
위에서 언급했듯, 재귀로 구현하면 Back Traking 로직을 구현할 필요가 없음

그럼 한번 간단한 JS 코드를 통해 살펴볼까요?

코드

/** graph 객체, 연결된 노드를 포함하고 있음 */
const graph = {
  A: ["B", "C", "D"],
  B: ["A", "E"],
  C: ["A"],
  D: ["A", "F"],
  E: ["B"],
  F: ["D"],
};

우선 graph 객체부터 예시로 생성해보도록 하겠습니다.

/** 노드를 방문기록을 담고 있는 visited 배열 */
const visited = {};
Object.keys(graph).map((key) => (visited[key] = false)); // { A: false, B: false, C: false, D: false, E: false, F: false }

그 다음, 해당 노드의 방문기록을 표시할 visited 객체를 만들겠습니다.

/** dfs 구현: graph, 방문할 node, 방문기록 visited 객체가 필요함 */
function dfs(graph, node, visited) {
  /** dfs함수가 실행되면 방문한 node를 true로 설정 */
  visited[node] = true;

  /** 방문한 노드 출력 */
  console.log(node);

  /** 방문한 노드의 연결된 자식노드를 탐색 */
  graph[node].forEach((neighbor) => {
    /** 자식 노드를 방문한 적이 없다면 dfs 재귀 호출로 방문하여 그 다음 자식노드를 탐색 */
    if (!visited[neighbor]) {
      dfs(graph, neighbor, visited);
    }
  });
}

/** 루트 노드인 A부터 탐색 */
dfs(graph, "A", visited);

dfs를 구현로직까지 완성!!, 아래는 전체코드 입니다.

const graph = {
  A: ["B", "C", "D"],
  B: ["A", "E"],
  C: ["A"],
  D: ["A", "F"],
  E: ["B"],
  F: ["D"],
};

const visited = {};
Object.keys(graph).map((key) => (visited[key] = false));

function dfs(graph, node, visited) {
  visited[node] = true;

  console.log(node);

  graph[node].forEach((neighbor) => {
    if (!visited[neighbor]) {
      dfs(graph, neighbor, visited);
    }
  });
}

dfs(graph, "A", visited);

해당 코드를 실행하게 되면 위 사진은 결과는 A -> B -> E -> C -> D -> F가 나오게 됩니다.

장점

1. 구현 간단

재귀, 스택 자료구조를 사용해 직관적으로 구현이 가능하다.

2. 메모리 효율적(스택 한정)

BFS와 비교했을 때, 전체 그래프를 저장하지 않고 현재 경로만 기록하므로 메모리 사용량이 상대적으로 적다.
특히 노드 개수가 많고 간선이 적은 희소 그래프에 효율적이다.

3. 특정 경로 탐색에 유리

경로 기반 문제(예: 미로 찾기, 경로 존재 여부)에서 깊이 우선으로 탐색하므로 적합하다.
도착 지점에 도달하면 즉시 탐색을 종료할 수 있어 빠르게 결과를 얻을 수 있다.

단점

1. 깊이가 너무 깊으면 비효율적

그래프의 깊이가 매우 깊을 수록 스택오버플로우가 발생할 수 있다.

2. 최적 경로 보장 X

경로를 우선 탐색하기 때문에, 목표 지점까지 도달하는데 가장 짧은 경로(최적 경로)를 찾는데는 적합하지 않다.
가중치가 없는 최단 경로를 찾기 위해선 BFS가 더 적합하다.

3. 모든 경로 탐색에 비효율적

모든 경로를 탐색해야 할 경우, DFS는 특정 방향으로 계속 들어가므로 경로 탐색 시간이 오래걸릴 수 있다.

마무리

dfs에 대해 알아보았는데 동작과정은 생각보다 어렵지는 않아서 이해하는데 어려움은 없었던 것 같습니다. 분명 이상하게도 고1 수업시간에 배웠을 때는 하나도 이해 안됐었는데 학년이 올라가서 이해가 되는 건 참 신기한 것 같습니다. 하하 그럼 저는 dfs 알고리즘 풀러가보겠습니다. 아 그리고, 프로그래머스 무인도 여행 풀어보세요! dfs로 푸는 문제입니당

그래프 탐색 알고리즘 - DFS

개요

그래프 탐색이란?

dfs란?

동작과정

코드

장점

단점

마무리

레퍼런스