DOVI-LOG | 그래프 탐색 알고리즘

개요

DFS에 대해 알아보았으니 BFS도 알아봐야겠죠? 빨리 공부해봅시다.

bfs란?

dfs가 경로기반의 문제를 해결할 때 사용하는 거라면, bfs는 목표 기반의 그래프 탐색 알고리즘입니다. 노드 간의 최단 경로를 찾거나 공간 문제에서 최소 단계로 목표에 도달하는데 사용됩니다.

구현 방식으로는 일반적으로 큐로 구현할 수 있습니다. 재귀로도 할 수 있는데 제가 둘다 구현해본 결과, 재귀로 풀어도 결국엔 큐를 사용하기 때문에 재귀보단 큐가 빌 때까지 반복문을 돌려서 푸는게 훨씬 간편하고 이해하기 편하더라고요 ㅎㅎ 재귀로 푸냐 큐로 푸냐의 문제보단 재귀냐 반복문이냐의 차이가 더 적절한 것 같네요.

동작과정

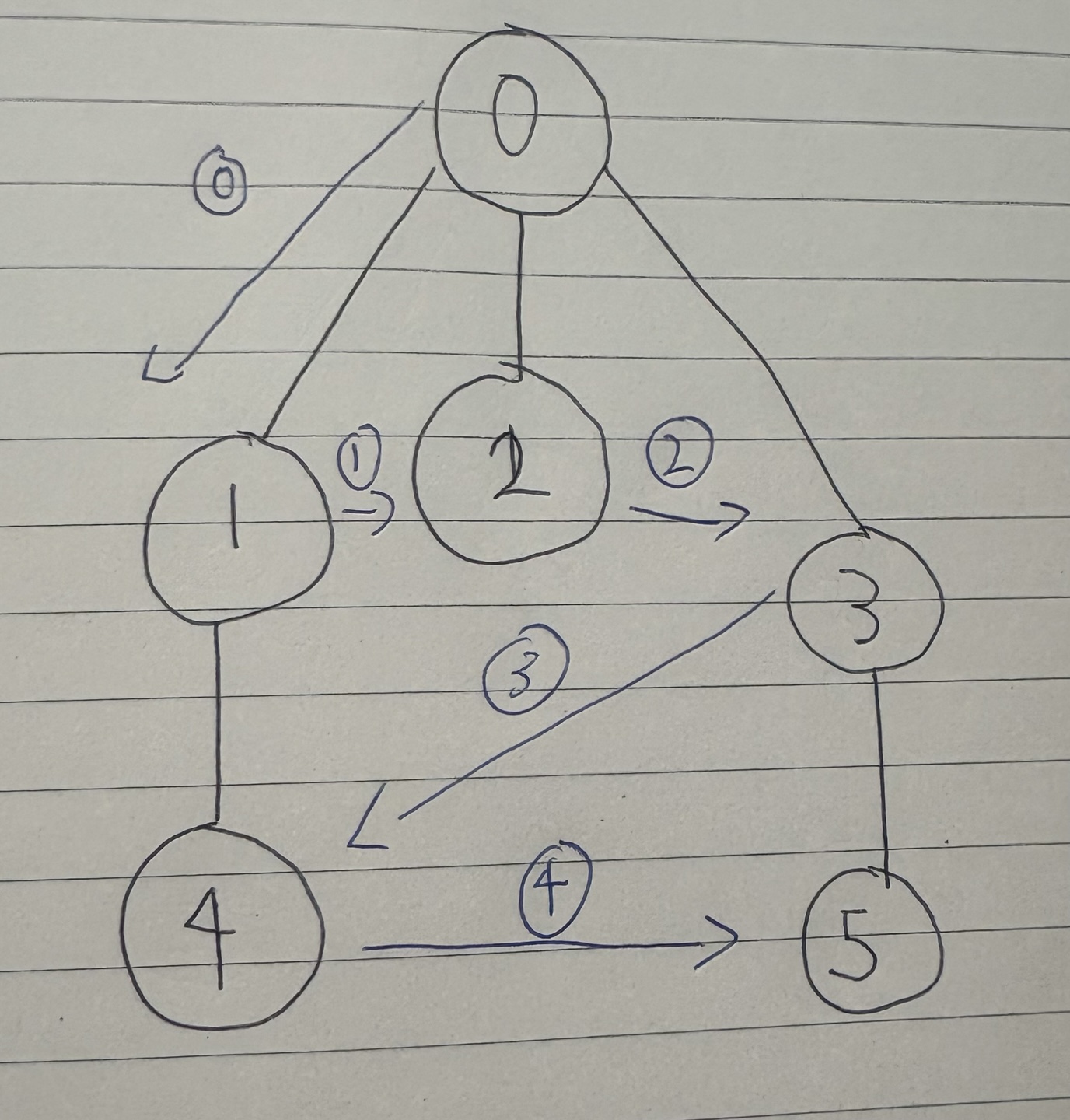
bfs 사진 위 사진도 dfs 글처럼 제가 그린 트리입니다 ㅎㅎ, 이번엔 큐로 설명을 해야겠군요. 엄청 간단해요

예시 트리

   A
 / | \
B  C  D
|     |
E     F

1. 시작노드를 큐에 넣고 순회

이때 visited 배열에 방문기록을 해놓는다.
queue: [A]

2. 큐에서 front 노드를 추출

shift 메서드를 사용해 추출과 동시에 queue에서 제거
해당 노드의 연결노드들을 queue에 담는데, 방문하지 않은 자식노드들만 삽입
queue: [B, C, D]

3. 반복

queue: [C, D, E] -> [D, E] -> [E, F] -> [F] -> []

코드

/** 그래프 */
const graph = [[1, 2, 3], [0, 4], [0], [0, 5], [1], [3]];

일단 예제로 그래프 배열부터 만들어볼게요

/** graph 배열길이만큼 visited 배열 생성 */
const visited = {};
graph.forEach((\_, idx) => (visited[idx] = false));

dfs처럼 방문 기록을 담고 있는 visited 객체가 필요합니다.

// queue 배열에 루트 노드 추가
const queue = [0];
// graph에 방문했음을 기록
visited[queue[0]] = true;

function bfs(graph, queue, visited) {
  while (queue.length > 0) {
    // queue 맨 앞 값 추출 및 삭제
    const node = queue.shift();
    console.log(node);

    // 그래프에서 해당 노드의 자식노드값 참조
    graph[node].forEach((neighbor) => {
      // 방문하지 않은 연결노드만 queue에 추가
      // 그리고 노드를 방문했음을 기록
      if (!visited[neighbor]) {
        queue.push(neighbor);
        visited[neighbor] = true;
      }
    });
  }
}

그 다음, 위 코드처럼 bfs를 구현하면 끝!, 아래는 전체코드입니다.

const graph = [[1, 2, 3], [0, 4], [0], [0, 5], [1], [3]];

const visited = {};
graph.forEach((_, idx) => (visited[idx] = false));

const queue = [0];
visited[queue[0]] = true;

function bfs(graph, queue, visited) {
  while (queue.length > 0) {
    const node = queue.shift();
    console.log(node);

    graph[node].forEach((neighbor) => {
      if (!visited[neighbor]) {
        queue.push(neighbor);
        visited[neighbor] = true;
      }
    });
  }
}

bfs(graph, queue, visited);

재귀로도 구현해봤다고 위에 말씀드렸는데 아래 코드가 재귀로 구현한 bfs입니다.

const graph = [[1, 2, 3], [0, 4], [0], [0, 5], [1], [3]];

const visited = {};
graph.forEach((_, idx) => (visited[idx] = false));

const queue = [0];

function bfs(graph, queue, visited) {
  if (queue.length === 0) {
    return;
  }

  const node = queue.shift();
  visited[node] = true;

  console.log(node);

  graph[node].forEach((neighbor) => {
    if (!visited[neighbor]) {
      queue.push(neighbor);
    }
  });

  bfs(graph, queue, visited);
}

bfs(graph, queue, visited);

두 코드 둘다 큐를 사용하기에 로직 상의 차이는 크지 않다는 것을 알 수 있습니다. 위에서 언급했듯, 반복문을 돌리는 것이 bfs의 이해와 구현면에서 더 나은 것 같군요!

장점

1. 최단 경로 탐색에 유리

만약 간선 가중치가 모두 동일할 때만 최단 경우가 보장됨 => 그렇지 않으면 오히려 단점이 됨
ex) 그래프에서 두 노드 간의 최소 이동 횟수를 구할 때 사용됨

2. 모든 경로를 균등하게 탐색

깊이보다 너비를 우선 탐색(해당 레벨의 모든 노드를 우선 탐색)하므로, 특정 조건을 만족하는 경로를 빠르게 찾을 수 있음.

3. 순환 검출 및 연결성 확인

그래프가 연결 그래프인지 확인 or 사이클 존재 여부를 확인할 때 적합함.

4. 루프 방지에 용이

visited를 사용해 노드의 방문기록을 가지고 있어서 중복 방문없이 탐색이 가능함.
이는 dfs와 동일한 장점

단점

1. 높은 메모리 사용량

탐색할 때 노드를 큐에 저장하기에, 노드가 많을수록 메모리 사용량도 급격히 증가함.
시간복잡도 면에선 dfs와 동일하지만, 실제 실행 속도에선 큐 관리로 인해 느릴 수 있음.

2. 가중치가 있는 그래프에 부적합

간선에 가중치가 있는 경우, 위에서 언급했듯, bfs는 최단경로를 보장 X
해결하려면 다익스트라 알고리즘 같은 가중치를 고려한 알고리즘이 필요함.

마무리

dfs를 알고나니 bfs의 이해도 큰 어려움없이 수월하게 공부할 수 있었습니다. 아직 bfs 알고리즘 문제는 풀어보진 않아서 이 글 쓰고 바로 풀어보도록 하겠습니다. 그럼 바이바이!!

그래프 탐색 알고리즘 - BFS

개요

bfs란?

동작과정

코드

장점

단점

마무리

레퍼런스